Otra de las utilidades de dominar los conceptos sobre el Plano cartesiano radica en que, a partir de la ubicación de las coordenadas de dos puntos es posible calcular la distancia entre ellos.
Cuando los puntos se encuentran ubicados sobre el eje x (de las abscisas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas (x2 – x1) .
Ejemplo:
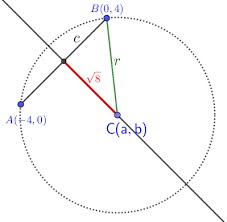
La distancia entre los puntos (–4, 0) y (5, 0) es 5 – (–4) = 5 +4 = 9 unidades.
Cuando los puntos se encuentran ubicados sobre el eje y (de las ordenadas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas.
Ahora, si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:
Distancia001(1)
Para demostrar esta relación se deben ubicar los puntos P1(x1, y1) y P2(x2, y2) en el sistema de coordenadas, luego formar un triángulo rectángulo de hipotenusa P1P2 y emplear el Teorema de Pitágoras.
Ejemplo:
Calcula la distancia entre los puntos P1(7, 5) y P2(4, 1)
Distancia002
Distancia003
Distancia004
Distancia005
d = 5 unidades
Demostración
Sean P1 (x1, y1) y P2 (x2, y2) dos puntos en el plano.
La distancia entre los puntos P1 y P2 denotada por d = Distancia006 esta dada por:
Distancia008(1)
En la Figura 1 hemos localizado los puntos P1 (x1, y1) y P2 (x2, y2) así como también el segmento de recta Distancia009
Distancia010
Figura 1
Al trazar por el punto P1 una paralela al eje x (abscisas) y por P2 una paralela al eje y (ordenadas), éstas se interceptan en el punto R, determinado el triángulo rectángulo P1RP2 y en el cual podemos aplicar el Teorema de Pitágoras:
Distancia011
Pero: Distancia013 ;
Distancia015 y Distancia016
Luego, Distancia018
Distancia020
En la fórmula (1) se observa que la distancia entre dos puntos es siempre un valor positivo.
El orden en el cual se restan las coordenadas de los puntos P1 y P2 no afecta el valor de la distancia
Ejemplo (demostración)
Con este vídeo podrás apoyarte para entender mejor este proceso
RECTAS TANGENTES DE LA CIRCUNFERENCIA
Cuando una recta toca a una circunferencia en un punto, la recta se llama tangente. Las rectas tangentes a la circunferencia tienen especial interés en la geometría.
Teorema
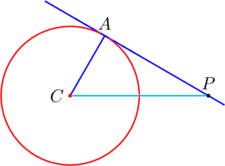
El radio de una circunferencia trazado al punto de tangencia es perpendicular a la tangente.
Demostración
Por la desigualdad del triángulo, \AC+ \AP > \CP, para cualquier punto P que esté sobre la tangente, distinto de A, siendo A el punto de tangencia. En otras palabras, para cualquier punto P diferente de A, la distancia desde P hasta el centro de la circunferencia es mayor que el radio. Es decir, el radio es la menor distancia desde el centro de la circunferencia a la recta tangente, y por eso el radio es perpendicular a la recta tangente.
Otra forma de dar este mismo resultado es:
Corolario
La perpendicular a una recta tangente a una circunferencia en el punto de tangencia pasa por el centro de la circunferencia.
Teorema
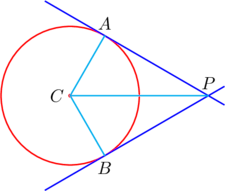
Dos tangentes a una circunferencia que pasan por un mismo punto P externo a la circunferencia y con puntos de tangencia en A y B, respectivamente, cumplen: |AP| = |BP|.
Teorema
Trazamos dos radios a los puntos de tangencia y el segmento de recta que va del centro de la circunferencia al punto P. Así hemos formado dos triángulos rectángulo: CAP y CBP siendo \ CAP y \CBP ángulos recto. En estos triángulos los lados
CA y CB tienen la misma medida al ser ambos radios de la misma circunferencia.